设数列{an}满足:a1 2a2 3a3 … nan=2n(n∈N*).(1)求数列{an}的通项公式;(2)设bn=n2an,求数列{bn}的前n项和Sn.
设数列{an}满足:a1 2a2 3a3 … nan=2n(n∈N*).(1)求数列{an}的通项公式;(2)设bn=n2an,求数列{bn}的前n项和Sn.
发布时间:2025-05-20 23:07:52
设数列{an}满足:a1 2a2 3a3 … nan=2n(n∈N*).(1)求数列{an}的通项公式;(2)设bn=n2an,求数列{bn}的前n项和Sn.
 (n≥2),在①中令n=1得a1=2,∴an=
(n≥2),在①中令n=1得a1=2,∴an=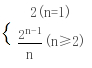 (2)∵bn=
(2)∵bn=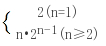 .则当n=1时,S1=2∴当n≥2时,Sn=2 2×2 3×22 … n×2n-1则2Sn=4 2×22 3×23 … (n-1)•2n-1 n•2n相减得Sn=n•2n-(2 22 23 … 2n-1)=(n-1)2n 2(n≥2)又S1=2,符合Sn的形式,∴Sn=(n-1)•2n 2(n∈N*)
.则当n=1时,S1=2∴当n≥2时,Sn=2 2×2 3×22 … n×2n-1则2Sn=4 2×22 3×23 … (n-1)•2n-1 n•2n相减得Sn=n•2n-(2 22 23 … 2n-1)=(n-1)2n 2(n≥2)又S1=2,符合Sn的形式,∴Sn=(n-1)•2n 2(n∈N*)